2 years ago
ABC is an inscribed triangle and chord AD bisects angle A and cuts BC at P. Prove: (AD)/(CD)=(AC)/(PC).
GIven: Inscribed △ ABC, chord AD bisects ∠ A and cuts BC at P; chord CD
Prove: (AD)/(CD)=(AC)/(PC).
Statements
1.(see above)
2. ∠ D=∠ D
3.
4. ∠ BCD=∠ DAB
5.
6. △ ACD-△ CPD
7. (AD)/(CD)=(AC)/(PC)
Reasons
1.Given
2.
3.Defintion of angle bisectors
4.
5.Substitution
6.
7.
GIven: Inscribed △ ABC, chord AD bisects ∠ A and cuts BC at P; chord CD
Prove: (AD)/(CD)=(AC)/(PC).
Statements
1.(see above)
2. ∠ D=∠ D
3.
4. ∠ BCD=∠ DAB
5.
6. △ ACD-△ CPD
7. (AD)/(CD)=(AC)/(PC)
Reasons
1.Given
2.
3.Defintion of angle bisectors
4.
5.Substitution
6.
7.
1 Answers
Best Answer
Anh Staff answered 2 years ago
Anh Staff answered 2 years ago
Step1
∠D=∠ D
Here angle D is equal to itself, that is reflexive property.
Given, AD bisects angle A, so by definition of angle bisector
∠ CAD=∠ DAB
Step2
From the picture, we see that angle BCD and angle DAB are two inscribed angles with the same base points on the circle.
So they are equal.
∠ BCD=∠DAB
If we substitute angle DAB by angle BCD in
∠ CAD=∠ DAB
We get:
∠ BCD=∠ CAD
So triangle ACD and triangle CPD has two pairs of angles equal. So they are ~ilar by AA property.
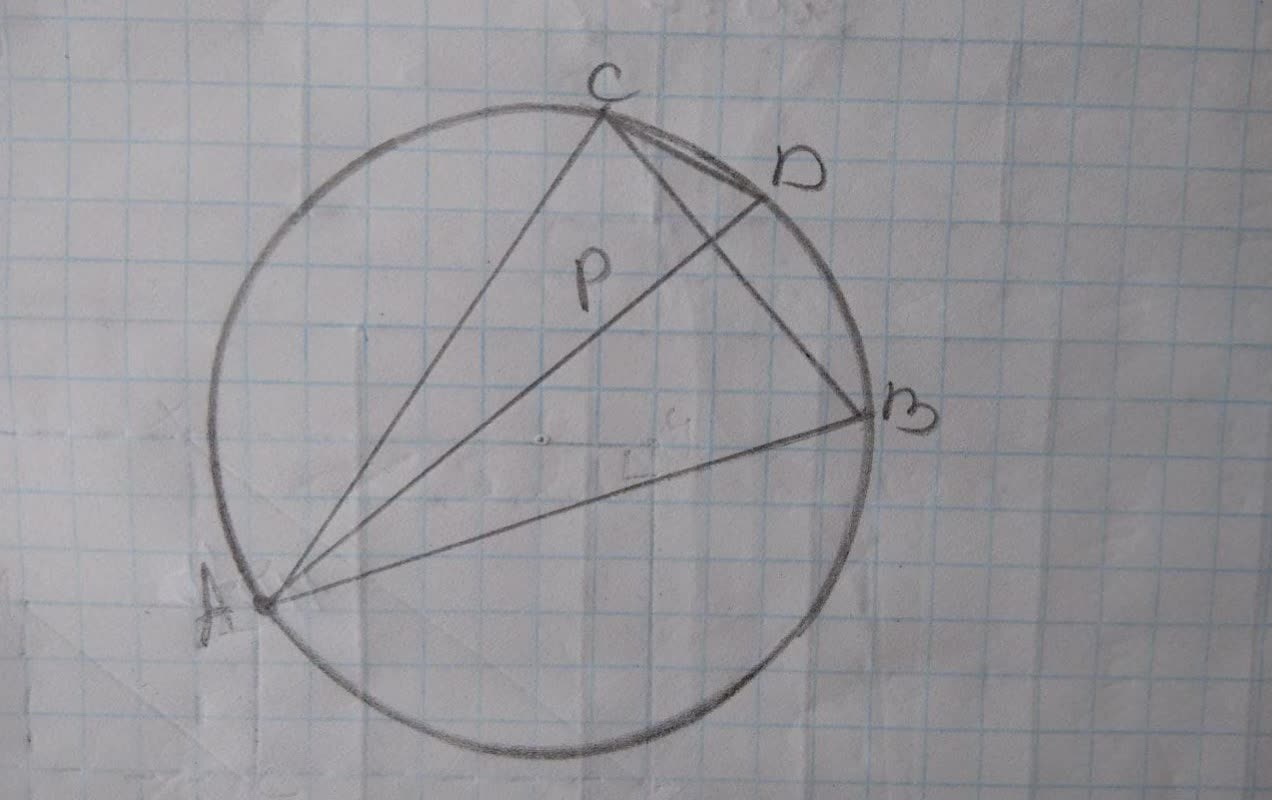Corollary 57-1 If two angles of one triangle are equal respectively to two angles of another, then the triangles
are ~ilar. (a.a.)
So,
(AD)/(CD)=(AC)/(PC)
by C.S.S.T.P, - corresponding sides of ~ilar triangles are proportional.
Answer:
2) Reflexive property
3) ∠ CAD=∠ DAB
4)Inscribed angles with same base points
5) ∠ BCD=∠ CAD
6) a.a
7) C.S.S.T.P.
Corollary 57-1 If two angles of one triangle are equal respectively to two angles of another, then the triangles
are ~ilar. (a.a.)
So,
(AD)/(CD)=(AC)/(PC)
by C.S.S.T.P, - corresponding sides of ~ilar triangles are proportional.
Answer:
2) Reflexive property
3) ∠ CAD=∠ DAB
4)Inscribed angles with same base points
5) ∠ BCD=∠ CAD
6) a.a
7) C.S.S.T.P.