2 years ago
Look at the triangulation of convex polygons again. Prove following statements:
Any triangulation of a convex n-polygon subdivides it into n - 2 triangles.
For example, every triangulation of a convex pentagon has 5 - 2=3 triangles, and every triangulation of a hexagon has 6-2=4 triangles
Any triangulation of a convex n-polygon subdivides it into n - 2 triangles.
For example, every triangulation of a convex pentagon has 5 - 2=3 triangles, and every triangulation of a hexagon has 6-2=4 triangles
1 Answers
Best Answer
admin Staff answered 2 years ago
admin Staff answered 2 years ago
Step1
In the question we have to prove that any triangulation of a convex n-polygon subdivides it into n - 2 triangles.
Step2
A convex polygon can be defined as a polygon whose interior angles are less than 180°.
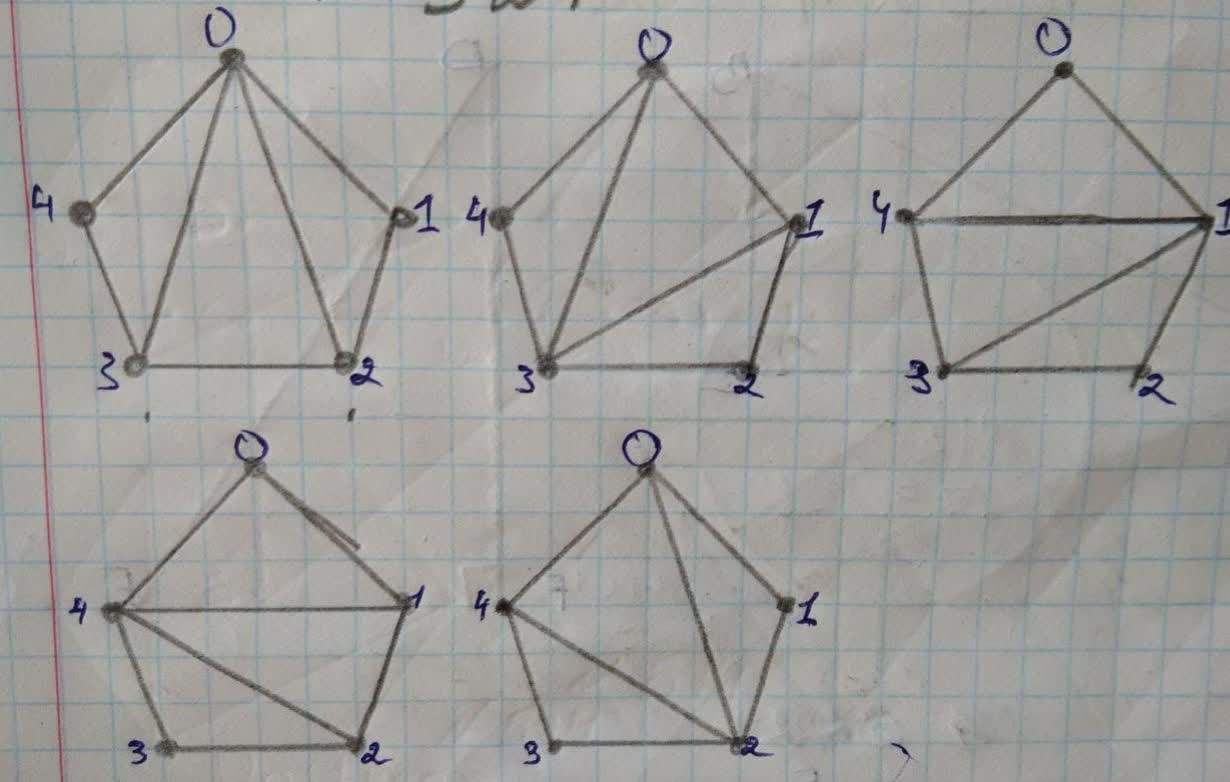A triangulation of a convex polygon is given by drawing diagonals between non-adjacent vertices or we can
say corners , also whose diagonal never intersect another diagonal (except at a vertex), until all possible ways of drawing diagonals have been used.
For proof of triangulation of a convex n-polygon subdiides it into n- 2 triangles we will sketch polygon of 5
and 6 sides and show every possible diagonal.
when n=5
as we can clearly see there are only 3 triangles possible in a convex pentagon, which proves the
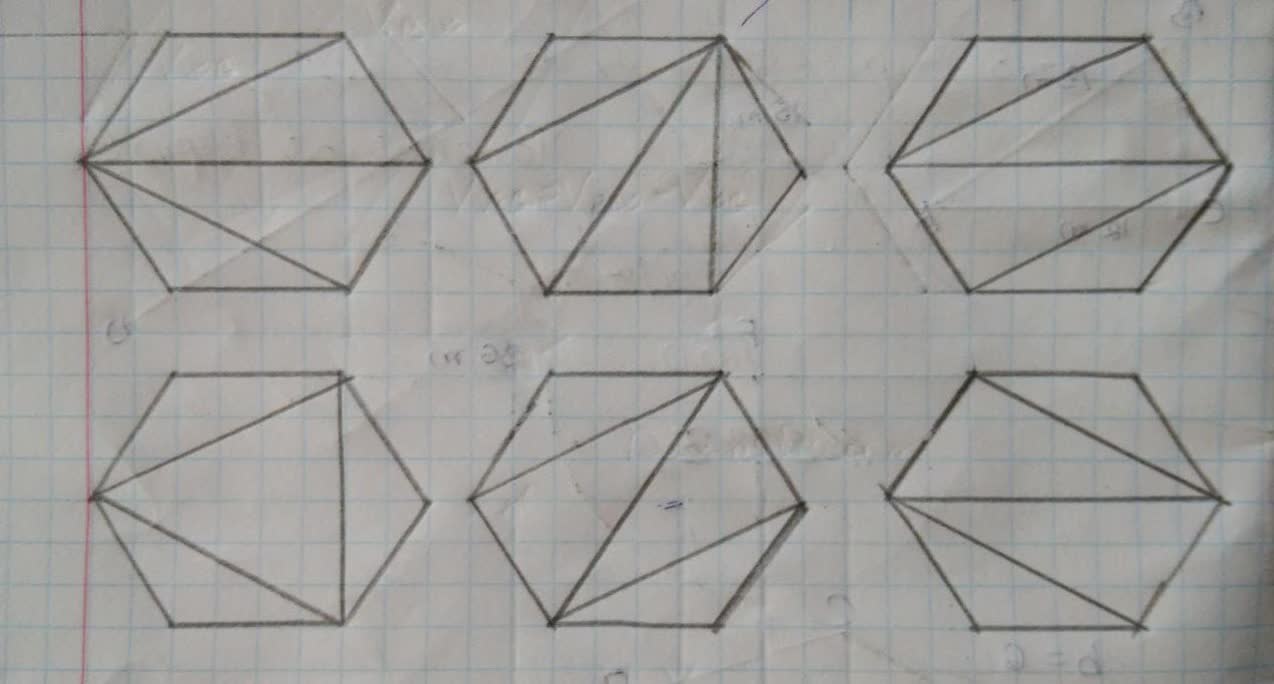statement any triangulation of a convex n-polygon subdivides it into n - 2 triangles.
when n=6
as we can clearly see there are only 3 triangles possible in a convex hexagon, which proves the
statement any triangulation of a convex n-polygon subdivides it into n - 2 triangles.
![]()
![]()
A triangulation of a convex polygon is given by drawing diagonals between non-adjacent vertices or we can
say corners , also whose diagonal never intersect another diagonal (except at a vertex), until all possible ways of drawing diagonals have been used.
For proof of triangulation of a convex n-polygon subdiides it into n- 2 triangles we will sketch polygon of 5
and 6 sides and show every possible diagonal.
when n=5
as we can clearly see there are only 3 triangles possible in a convex pentagon, which proves the
statement any triangulation of a convex n-polygon subdivides it into n - 2 triangles.
when n=6
as we can clearly see there are only 3 triangles possible in a convex hexagon, which proves the
statement any triangulation of a convex n-polygon subdivides it into n - 2 triangles.