3 years ago
triangle ABC is a right triangle with its right angle at C. The bisector of angle B intersects AC at D. The bisector of the exterior angle at B intersects AC at E. If BD= 15 and BE=20, what are the lengths of triangle ABC?
1 Answers
Best Answer
brothersosborneticketscalgary Staff answered 3 years ago
brothersosborneticketscalgary Staff answered 3 years ago
Step 1
Using basic properties of triangles we can solve this question.
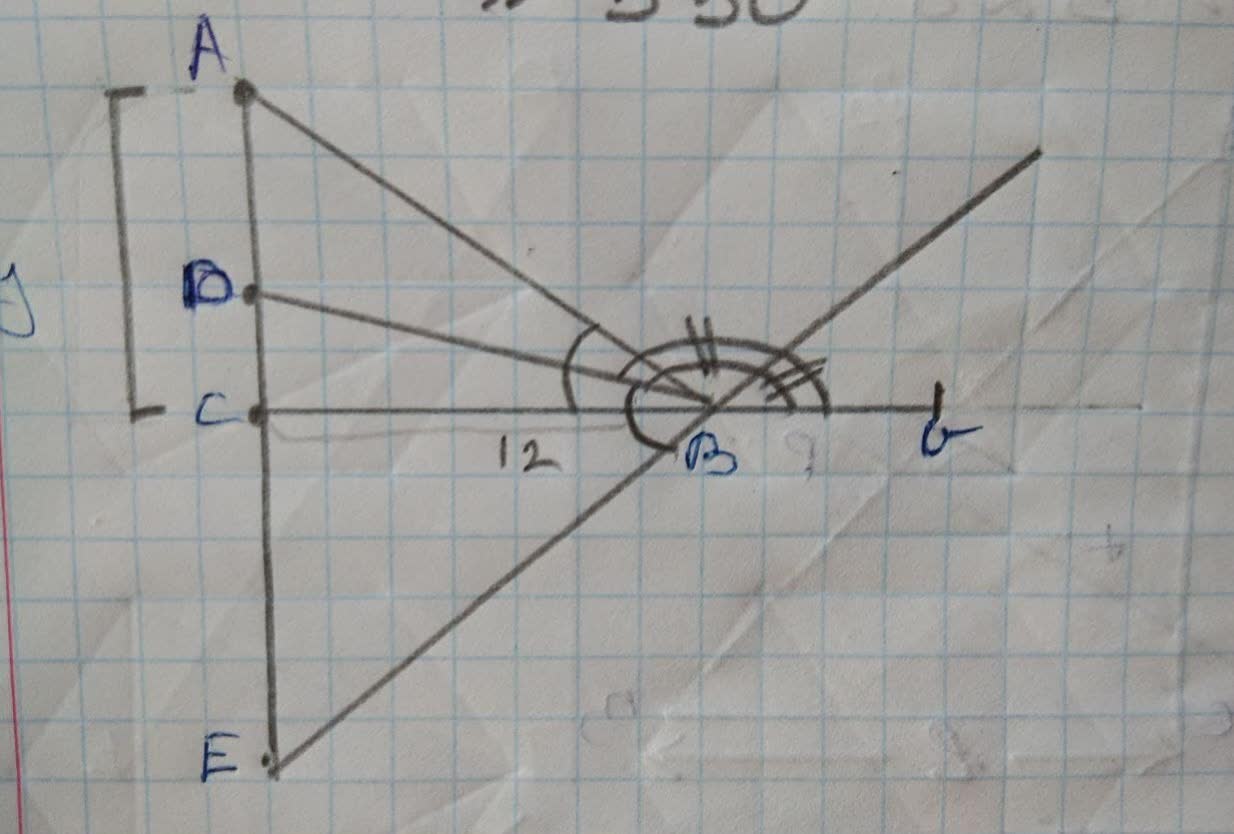Step2
angle abc is bisected by bd
angle abg is bisected by be
angle dbe=90(half of a angle in a straight line)
bd=15cm
be=20cm
By pythagoras theorem,
de=25cm
Let de=xcm
be=sqrt(be^(2)-ce^(2))
=sqrt(bd^(2)-dc^(2))
=12cm
Step 3
∠ dbc=(dc)[bc)
=(9)/(12)
dc=x
ec=25-x
be^(2)-ce^(2)=bd^(2)-x^(2)
x=dc
=9cm
∠ abc=2∠ 0bc
=(24)/(7)
(24)/(7)=(y)/(12)
y=(24* 12)/(7)
ac=(288)/(7)
By pythagoras theorem
ac^(2)+bc^(2)=ab^(2)
ab=(300)/(7)
Step2
angle abc is bisected by bd
angle abg is bisected by be
angle dbe=90(half of a angle in a straight line)
bd=15cm
be=20cm
By pythagoras theorem,
de=25cm
Let de=xcm
be=sqrt(be^(2)-ce^(2))
=sqrt(bd^(2)-dc^(2))
=12cm
Step 3
∠ dbc=(dc)[bc)
=(9)/(12)
dc=x
ec=25-x
be^(2)-ce^(2)=bd^(2)-x^(2)
x=dc
=9cm
∠ abc=2∠ 0bc
=(24)/(7)
(24)/(7)=(y)/(12)
y=(24* 12)/(7)
ac=(288)/(7)
By pythagoras theorem
ac^(2)+bc^(2)=ab^(2)
ab=(300)/(7)