2 years ago
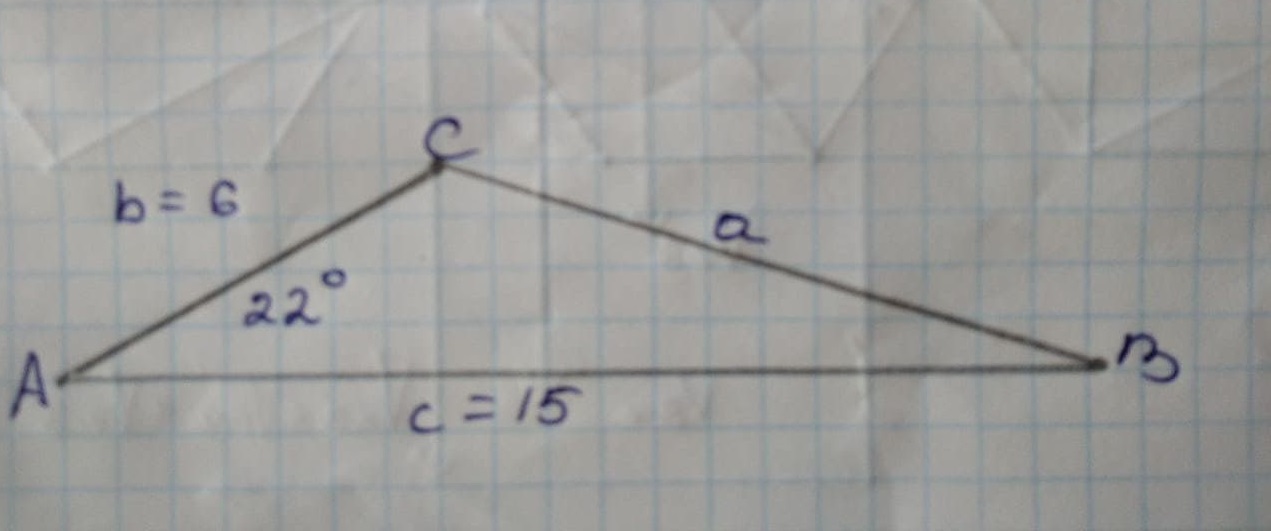
Use the Law of Cosines to solve the triangles. Round lengths to the nearest tenth and angle measures to the
nearest degree. PLEASE solve both of these triangles. Thank you!
1 Answers
Best Answer
celticthundertourwollongong Staff answered 2 years ago
celticthundertourwollongong Staff answered 2 years ago
using Cosine rule, cosA =(b^(2)+c^(2)-a^(2))/(2bc)
-> cos(22)=((6)^(2)+(15)^(2)-a^(2))/(2(6)(15))
-> 0/9272=(36+225-a^(2))/(180)
-> 166.893=261-a^(2)
-> a^(2)=94.1069
-> a=9.7009
-> ~ 10
using Sine rule, (sin A)/(a)=(sinB)/(b)
-> (sin(22))/(10)=(sinB)/(6)
-> sin B=(6sin(22))/(10)
-> B~ 13°
using angle sum property of a triangle,
C = 180- (A+B)
= 180 - (22 + 13)
= 145°
Therefore, a=10,B=13°,C=145°